
With few members at the high and low ends and many in the middle.īecause they occur so frequently, there is an unfortunate tendency to invoke normal distributions in situations where they may not be applicable. Many commonĪttributes such as test scores, height, etc., follow roughly normal distributions, Variance tends to the normal distribution. Of variates with any distribution having a finite mean and This theorem states that the mean of any set To a surprising result known as the central limit Normal distributions have many convenient properties, so random variates with unknown distributions are often assumed to be normal, especially in physics and astronomy.Īlthough this can be a dangerous assumption, it is often a good approximation due Want to learn more about calibrating your senses and thinking critically? Check out Bayes Theorem: A Framework for Critical Thinking.Where erf is the so-called error function. The challenging part, indeed, is figuring out whether the distribution is normal or not. Since all we need to describe any normal distribution is the mean and standard deviation, this rule holds for every normal distribution in the world! Knowing this rule makes it very easy to calibrate your senses. So, the chance of seeing someone with a height between 65 and 68.5 inches would be: _.ģ4%! It's exactly the same as our first example. Try doing the same for female heights: the mean is 65 inches, and standard deviation is 3.5 inches. Remember, you can apply this on any normal distribution. So the outer edges (that is, heights below 58 and heights above 82) together make (100% - 99.7%) = 0.3%. Here, we use also the final property: everything must sum to 100%. Both outer edges have the same %.Īnd now your final (and hardest test): What's the chance of seeing someone with a height greater than 82 inches? What's the chance of seeing someone with a height between 62 and 66 inches? It's 34%! We leverage both the properties: the distribution is symmetric, which means chances for (66-70) inches and (70-74) inches are both 68/2 = 34%. What's the chance of seeing someone with a height between between 5 feet 10 inches and 6 feet 2 inches? (That is, between 70 and 74 inches.) Now for the fun part: Let's apply what we've just learned. To continue our example, the average American male height is 5 feet 10 inches, with a standard deviation of 4 inches. It says: 68% of the population is within 1 standard deviation of the mean.ĩ5% of the population is within 2 standard deviation of the mean.ĩ9.7% of the population is within 3 standard deviation of the mean. The 68-95-99 rule is based on the mean and standard deviation. Together, the mean and the standard deviation make up everything you need to know about a distribution. And even fewer are three standard deviations away (or further). Fewer observations are two standard deviations from the mean. Most observations fall within one standard deviation of the mean. This tells you how rare an observation would be. For example, the average of these three numbers: 1, 2, 3 = (1 + 2 + 3) / 3 = 2 Most people just call this "the average." It's what you get if you add up the value of all your observations, then divide that number by the number of observations. There's equal mass before and after the peak.Īnother important property is that we don't need a lot of information to describe a normal distribution. You can reduce lots of complicated mathematics down to a few rules of thumb, because you don't need to worry about weird edge cases.įor example, the peak always divides the distribution in half. This distribution is exciting because it's symmetric – which makes it easy to work with. A lot of things follow this distribution, like your height, weight, and IQ.

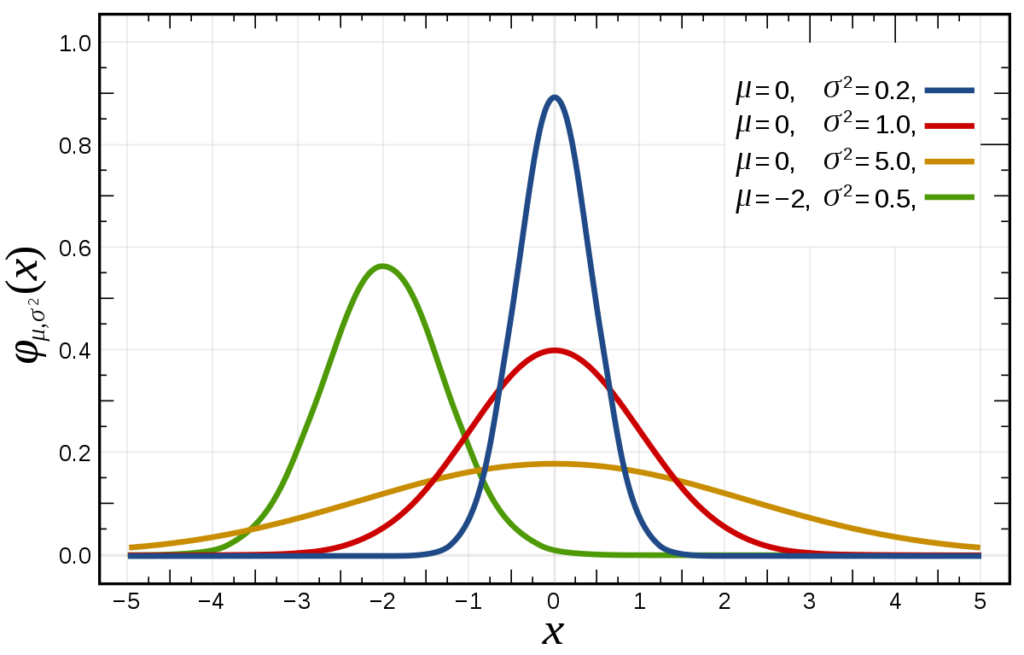
They are represented by a bell curve: they have a peak in the middle that tapers towards each edge. Today, we're interested in normal distributions. In some cases, 10x above average is common. Your answers to the two questions above are different, because the distribution of data is different. How often would you expect to meet someone who earns 10x as much as Mason?Īnd now, how often would you expect to meet someone who is 10x as tall as Mason?
He's an average American 40-year-old: 5 foot 10 inches tall and earning $47,000 per year before tax.


 0 kommentar(er)
0 kommentar(er)
